Acid dissociation constant
Editor-In-Chief: C. Michael Gibson, M.S., M.D. [1]
Overview
An acid dissociation constant, denoted by Ka, is an equilibrium constant for the dissociation of a weak acid. According to the Brønsted-Lowry theory of acids and bases, an acid is a proton donor (HA, where H represents an acidic hydrogen atom), and a base is a proton acceptor. In aqueous solution, water can function as a base, as in the following general example.
- HA + H2O <math>\rightleftharpoons</math> A- + H3O+
Acid dissociation constants are also known as the acidity constant or the acid-ionization constant. The term is also used for pKa, which is equal to minus the decimal logarithm of Ka (cologarithm of Ka).
Definitions
Monoprotic acids
When an acid, HA, dissolves in water, some molecules of the acid 'dissociate' to form hydronium ions and the conjugate base, (A-), of the acid.
- <math>H A \rightleftharpoons H^{+} + A^{-}</math>
It is understood that <math>H^{+}</math> stands for the hydronium ion and that each species in this equilibrium may solvate to a greater or lesser extent. The acid dissociation constant is defined as
- <math>K_a = \frac{[\mbox{H}^+][\mbox{A}^- ]} {[\mbox{HA}]}</math>
where the square brackets are usually taken to signify concentration. <math>H_2 O</math> is omitted from these expressions because in dilute solution the concentration of water may be assumed to be constant. Values of <math>K_a</math> vary over many orders of magnitude, so it is common to take the logarithm to base ten of the value.
- <math>\operatorname{p}K_a = -\log_{10} K_a</math>
It is easier to compare the strengths of different acids by comparing <math>pK_a</math> values as they vary over a much smaller range.
Polyprotic acids
A polyprotic acid is one that has more than one proton to dissociate. Typical examples are malonic acid, which has two ionizable protons, and phosphoric acid, which has three. The constant for dissociation of the first proton may be denoted as <math>pK_{a1}</math> and the constants for dissociation of successive protons as <math>pK_{a2}</math>, etc.
It is generally true that successive pK values increase (Pauling's first rule).[1] For example, for a diprotic acid, <math>H_2 A</math>, the two equilibria are
- <math>H_2 A \rightleftharpoons HA^{-} + H^{+}</math>
- <math>HA^{-} \rightleftharpoons A^{2-} + H^{+}</math>
it can be seen that the second proton is removed from a negatively charged species. Since the proton carries a positive charge extra work is needed to remove it. Therefore <math>pK_{a2} > pK_{a1}</math>. There are a few exceptions to this rule which occur when there is a major structural change such as in the sequence
<math>VO_2^{+}(aq) \rightleftharpoons H_3 VO_4 + H^+</math> <math>pK_{a1} = 4.2</math> <math>H_3 VO_4 \rightleftharpoons H_2 VO_4^{-} + H^{+}</math> <math>pK_{a2} = 2.60</math> <math>H_2 VO_4^{-} \rightleftharpoons HVO_4^{2-} + H^{+}</math> <math>pK_{a3} = 7.92</math> <math>HVO_4^{2-} \rightleftharpoons VO_4^{3-} + H^{+}</math> <math>pK_{a4} = 13.27</math>
The pKs of vanadic acid, <math>H_3 VO_4</math>, follow Pauling's rule just like phosphoric acid (values below). All species in this series are tetrahedral, but <math>VO_2 \left( H_2 O \right)_4 ^{+}</math> is octahedral and <math>pK_{a2} < pK_{a1}</math>. [2]
Bases
Historically the equilibrium constant <math>K_b</math> for a base was defined as the dissociation constant of <math>BH</math>, the acid conjugate to the base, <math>B</math>. Ionic charges on <math>B</math> and/or <math>BH</math> are omitted here because the base may be a neutral species such as ammonia or a charged species such as the ethanoate ion (acetate).
- <math>B + H_2 O \rightleftharpoons BH + OH^{-}</math>
Using similar reasoning to that used before
- <math>K_b = \frac{[\mbox{BH}][\mbox{OH}^-]} {[\mbox{B}]}</math>
- <math>\operatorname{p}K_b = -\log_{10} K_b\,</math>
Now, the concentration of the hydroxide ion is related to the concentration of the hydronium by <math>K_w = \left[ H^{+} \right]\left[ OH^{-} \right]</math>, therefore
- <math>[\mbox{OH}^-] = \frac{K_w}{[\mbox{H}^+]}</math>;
<math>K_w</math> is the constant for the self-ionization of water. Substituting the expression for <math>\left[ OH^{-} \right]</math> into the expression for <math>K_b</math>
- <math>K_b = K_w \frac{ \left[ \mbox{BH} \right] }{ \left[ \mbox{B} \right] \left[ \mbox{H}^{+} \right] } = \frac{K_w}{K_a}</math>
It follows that
- <math>pK_b = pK_w - pK_a</math>
In water at 25 °C <math>pK_w</math> is 14 so then <math>pK_b = 14 - pK_a</math>.
In effect there is no need to define <math>pK_b</math> separately from <math>pK_a</math>, but it is done because <math>pK_b</math> values can be found in literature.
Protonation constants
The protonation constant for a substance <math>S</math>, is given by
- <math>S + H^{+} \rightleftharpoons SH</math>
- <math>K_{assoc} = \frac{[\mbox{SH}]} {[\mbox{S}][\mbox{H}^+]}</math>
Again, ionic charges are omitted from <math>S</math> and <math>SH</math>. <math>K_{assoc}</math> is an association constant.
- For any substance <math>\log_{10} \left( K_{assoc} \right) = pK_a</math>
Temperature dependence
All equilibrium constants vary with temperature according the van 't Hoff equation
- <math>\frac {d\ln K} {dT} = \frac{{\Delta H_m}^{\Theta}} {RT^2}.</math>
Thus, for exothermic reactions, (ΔH is negative) K decreases with temperature, but for endothermic reactions (ΔH is positive) K increases with temperature.
Usage
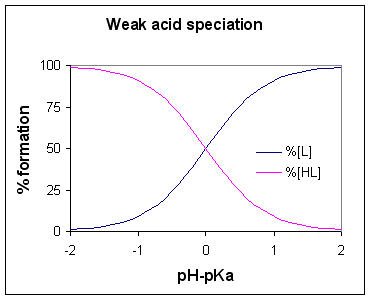
The pH of a solution of weak acid can be expressed in terms of the extent of dissociation. After rearranging the expression defining the dissociation constant, and putting pH = -log10[H+], one obtains
- <math>\mbox{pH} = \mbox{pK}_a - \log \frac{[HA]}{[A^-]}</math>
This is a form of the Henderson-Hasselbalch equation. It can be deduced from this expression that
- when the acid is 1% dissociated, that is, when <math>\frac{[HA]}{[A^-]} = 100</math>, pH = pKa – 2
- when the acid is 50% dissociated, that is, when <math>\frac{[HA]}{[A^-]} = 1</math>, pH = pKa
- when the acid is 99% dissociated, that is, when <math>\frac{[HA]}{[A^-]} = 0.01</math>, pH = pKa + 2
It follows that the range of pH within which there is partial dissociation of the acid is about pKa <math>\pm</math> 2.This is shown graphically at the right.
A weak acid may be defined as an acid with pKa greater than about -2. An acid with pKa = -2 would be 99% dissociated at pH 0, that is, in a 1M HCl solution. Any acid with a pKa less than about -2 is said to be a strong acid. Strong acids are said to be fully dissociated. There is no precise pKa value that distinguishes between strong and weak acids because strong acids, such as sulfuric acid, are associated in very concentrated solution.
On the pKa scale of acid strength, a large value indicates a very weak acid, and a small value indicates a not so weak one.
The pH of a solution of a weak acid can be easily calculated when the analytical concentration of the acid is known. See ICE table for details.
Some polyprotic acids can be treated as a set of individual acids. This is possible when successive pK values differ by 4 or more. For example with phosphoric acid
- H3PO4 <math>\rightleftharpoons</math> H2PO4- +H+, pKa1 = 2.15
- H2PO4- <math>\rightleftharpoons</math> HPO42- +H+, pKa2 = 7.20
- HPO42- <math>\rightleftharpoons</math> PO43- +H+, pKa3 = 12.37
Both the hydrogenphosphate and dihydrogenphosphate ions can be treated as acids in their own right. On the other hand, the two pKs for malonic acid are 2.51 and 5.05, so there are pH values at which both malonic acid and the hydrogenmalonate ion co-exist. More elaborate calculations are needed to calculate the composition of solutions of malonic acid.
Factors that determine the relative strengths of acids
Being an equilibrium constant, the acid dissociation constant Ka is determined
by the standard free energy difference ΔGo between the reactants and products, specifically, between the protonated (HA) and deprotonated (A−) forms of the substance.
Pauling's second rule[1] states that the value of the first pK for acids of the formula XOm(OH) n is approximately independent of n and X and is approximately 8 for m=0, 2 for m=1, -3 for m=2 and <-10 for m=3. This correlates with the oxidation state of the central atom, X: the higher the oxidation state the stronger the oxyacid. For example, pKa for HClO is 7.2, for HClO2 is 2.0, for HClO3 is -1 and HClO4 is a strong acid.
With organic acids inductive effects and mesomeric effects affect the pKs. The effects are summarised in the Hammett equation and subsequent extensions.
Structural effects can also be important. The difference between fumaric acid and maleic acid is a classic example. Fumaric acid is (E)-1,4-but-2-enedioic acid, a trans isomer, whereas maleic acid is the corresponding cis isomer, i.e. (Z)-1,4-but-2-enedioic acid (see cis-trans isomerism). Fumaric acid has pKas of approximately 3.5 and 4.5. By contrast, maleic acid has pKas of approximately 1.5 and 6.5. The reason for this large difference is that when one proton is removed from the cis- isomer (maleic acid) a strong intramolecular hydrogen bond is formed with the nearby remaining carboxyl group. This favors the formation of the maleate H+, and it opposes the removal of the second proton from that species. In the trans isomer, the two carboxyl groups are always far apart, so hydrogen bonding is not observed.
Importance of pKa values
The pKa value(s) of a compound influence many characteristics of the compound such as its reactivity, and spectral properties (colour). In biochemistry the pKa values of proteins and amino acid side chains are of major importance for the activity of enzymes and the stability of proteins. This property is of general importance in chemistry because ionization of a compound alters its physical behavior and macro properties such as solubility and lipophilicity. For example ionization of any compound will increase the solubility in water, but decrease the lipophilicity. This can be exploited in drug development to increase the concentration of a compound in the blood by adjusting the pKa of an ionizable group. This must be done with caution, however, since an ionized compound will pass less easily through cell membranes.
Acidity in nonaqueous solutions
Three properties of a solvent strongly affect acids and bases.
- A Protic solvent can form hydrogen bonds and will promote ionisation.
- A solvent with a high donor number is a strong Lewis base.
- A solvent with a high dielectric constant (Relative permittivity) will promote ionisation.
| Donor number | dielectric constant | |
|---|---|---|
| Acetonitrile | 14.1 | 37.5 |
| Dimethyl sulfoxide | 29.8 | 45 |
| Ethanol | 31.5 | 24.3 |
| Pyridine | 33.1 | 12.3 |
| Water | 18 | 81.7 |
For a given acid, pKa values will vary depending on solvent. The degree of dissociation of any acid increases with the increasing basicity of the solvent. On the other hand, dissociation is relatively less for solvents of low dielectric constant. An acidic solvent will also suppress dissociation of an acid. For example, hydrogen chloride is a weak acid, i.e. poorly ionised, when dissolved in the acidic solvent acetic acid.
Acidity scales have been developed for solvents aside from water, notably for dimethyl sulfoxide and acetonitrile.[3] It can be seen in the table above that DMSO is more basic than water, but its dielectric constant is less. DMSO is widely used as an alternative to water in evaluating acids and bases.
In solvents of low dielectric constant, ions tend to associate, which complicates the interpretation of pKas. In particular, in aprotic solvents the process of homoconjugation occurs when the conjugate base forms a hydrogen bond with the parent acid as in the following equilibrium
- HA + A- <math>\rightleftharpoons</math> HA2-
Typically HA2- would have the structure A---H---A. This process does not occur in water because H2O molecules are strong hydrogen bond donors and acceptors.
In acetonitrile solution, para-toluenesulfonic acid has a homoconjugation constant pKf, of -2.9.[4] This indicates that the toluenesulfonate anion has a strong tendency to form a hydrogen bond with the parent acid. Homoconjugation has the effect of enhancing the acidity of acids, lowering their effective pKas, by stabilizing the conjugate base. Due to homoconjugation, the proton-donating power of toluenesulfonic acid in acetonitrile solution is enhanced by a factor of nearly 800.
pKa of some common substances
Measurements are at 25ºC in water for those with a pKa at or above -1.76: Template:Col-begin-small Template:Col-2
- - 25.00: Fluoroantimonic acid
- - 15.00: Magic acid
- - 10.00: Fluorosulfuric acid
- - 10.00: Perchloric acid
- - 10.00: Hydroiodic acid
- - 9.00: Hydrobromic acid
- - 8.00: Hydrochloric acid
- - 3.00, 1.99: Sulfuric acid
- - 2.00: Nitric acid
- - 1.76: Hydronium ion
- 3.15: Hydrofluoric acid
- 3.60: Carbonic acid
- 3.75: Formic acid
- 4.04: Ascorbic acid (Vitamin C)
- 4.19: Succinic acid
- 4.20: Benzoic acid
- 4.63: Aniline*
- 4.76: Acetic acid
- 4.76: Dihydrogencitrate ion (Citrate)
- 5.21: Pyridine*
- 6.40: Monohydrogencitrate ion Citrate
- 6.99: Ethylenediamine*
- 7.00: Hydrogen sulfide, Imidazole* (as an acid)
- 7.50: Hypochlorous acid
- 9.25: Ammonia*
- 9.33: Benzylamine*
- 9.81: Trimethylamine*
- 9.99: Phenol
- 10.08: Ethylenediamine*
- 10.66: Methylamine*
- 10.73: Dimethylamine*
- 10.81: Ethylamine*
- 11.01: Triethylamine*
- 11.09: Diethylamine*
- 11.65: Hydrogen peroxide
- 12.50: Guanidine*
- 12.67: Monohydrogenphosphate ion (Phosphate)
- 14.58: Imidazole (as a base)
- 15.76: Water
- - 19.00 (pKb) Sodium amide
- 37.00: Lithium diisopropylamide (LDA)
- 45.00: Propane
- 50.00: Ethane
|}
* Listed values for ammonia and amines are the pKa values for the corresponding ammonium ions.
Further reading
- Atkins, Peter, and Loretta Jones. Chemical Principles: The Quest for Insight. 3rd ed. New York: W. H. Freeman and Company, 2005
- Housecroft, Catherine and Sharpe, Alan, Inorganic Chemistry, Prentice Hall, 2nd. edition, 2004. (Non-aqueous solvents)
See also
References
- ↑ 1.0 1.1 Template:Greenwood&Earnshaw p. 50
- ↑ Template:Greenwood&Earnshaw Chapter 22
- ↑ March, J. “Advanced Organic Chemistry” 4th Ed. J. Wiley and Sons, 1992: New York. ISBN 0-471-60180-2.
- ↑ Coetzee, J. F. and Padmanabhan, G. R., "Proton Acceptor Power and Homoconjugation of Mono- and Diamines", J. Amer. Chem. Soc.,1965, 87, 5005-5010.
External links
- Bordwell pKa Table in DMSO
- Shodor.org Acid-Base Chemistry
- Factors that Affect the Relative Strengths of Acids and Bases
- Purdue Chemistry
- Distribution diagrams of acids and bases (generation from p<math>K_{a}</math> values with free spreadsheet)
- SPARC Physical/Chemical property calculator
- List of Aqueous-Equilibrium Constants
- Free guide to pKa & logP interpretation and measurement
da:Syrestyrkekonstant de:Säurekonstante id:Konstanta disosiasi asam it:Costante di dissociazione acida lt:Rūgšties disociacijos konstanta nl:Zuurconstante no:Syrekonstanten fi:Happovakio sv:Syrakonstanten uk:PKa