Resonance (chemistry)
Template:Otheruses2
Resonance in chemistry is a tool used to represent and model certain types of non-classical molecular structures. Resonance is a key component of valence bond theory and arises when no single conventional model using only even number of electrons shared exclusively by two atoms can actually represent the observed molecule. There are two closely related but useful-to-distinguish meanings given to the term resonance. One of these has to do with diagrammatic representation of molecules using Lewis structures while the other has to do with the mathematical description of a molecule using valence bond theory. In both cases, resonance involves representing or modeling the structure of a molecule as an intermediate, average (a resonance hybrid) between several simpler but incorrect structures.
Resonance as a diagrammatic tool
A single Lewis structure often cannot represent the true electronic structure of a molecule. While one can only show an integral number of covalent bonds between two and only two atoms using these diagrams, one often finds that the experimentally deduced or calculated (from Quantum mechanics) structure of the molecule does not match any of the possible Lewis structures but rather has properties in some sense intermediate to these. Resonance structures are then employed to approximate the true electronic structure. Take the example of benzene (shown above, right). In a Lewis diagram, two carbons can be connected by one or two covalent bonds, but in the observed benzene molecule the bond lengths are longer than double bonds yet shorter than single bonds. More importantly, they are all equivalent, a fact no Lewis structure can explain. Therefore one calls the two Lewis structures canonical, contributing or resonating structures and the real molecule is considered to be their average, called a resonance hybrid. Resonance structures of the same molecule are connected with a double-headed arrow.
This form of resonance is simply a way of representing the structure graphically. It is only a notation and does not represent a real phenomenon. The individual resonance structures do not exist in reality: the molecule does not inter-convert between them. Instead, the molecule exists in a single unchanging state, intermediate between the resonance structures and only partially described by any one of them. This sharply distinguishes resonance from tautomerism. When it is said that a molecule is stabilized by resonance or that amides are less basic because the lone pair on nitrogen is involved in resonance with the carbonyl pi electron, no phenomenon is implied. What is meant is simply that the molecule behaves differently from what we expect by looking at its Lewis structure because the structure diagrammed does not represent the actual structure of the molecule. From this viewpoint, the terminology treating resonance as something that 'happens' is perhaps an unfortunate historical burden.
It is also not right to say that resonance occurs because electrons "flow" or change their place within the molecules. Such a thing would produce a magnetic field that is not observed in reality. However the application of an external magnetic field perpendicular to the plane of an aromatic ring causes the appearance of an opposing magnetic field, implying that the delocalised pi electrons are truly flowing, causing a current density which induces a magnetic field.
A vector analogy
An accurate analogy of resonance is given by the algebra of vectors. A vector r is written in component form as xi+yj+zk where x, y, and z are components and i, j, and k are the standard orthogonal Cartesian unit vectors. Just as the real vector r is neither x, nor y, nor z, but rather a combination of all three, a resonance hybrid is a conceptual combination of resonance structures. x, y, and z have no independent existence; they are considered only as a decomposition of r into easier-to-handle components, as is the case with resonance structures. In fact this analogy is very close to the reality, as will be made clear in the following section.
True nature of resonance
Though resonance is often introduced in such a diagrammatic form in elementary chemistry, it actually has a deeper significance in the mathematical formalism of valence bond theory (VB). When a molecule cannot be represented by the standard tools of valence bond theory (promotion, hybridisation, orbital overlap, sigma and pi bond formation) because no single structure predicted by VB can account for all the properties of the molecule, one invokes the concept of resonance.
Valence bond theory gives us a model for benzene where each carbon atom makes two sigma bonds with its neighbouring carbon atoms and one with a hydrogen atom. But since carbon is tetravalent, it has the ability to form one more bond. In VB it can form this extra bond with either of the neighbouring carbon atoms, giving rise to the familiar Kekulé ring structure. But this cannot account for all carbon-carbon bond lengths being equal in benzene. A solution is to write the actual wavefunction of the molecule as a linear superposition of the two possible Kekulé structures (or rather the wavefunctions representing these structures), creating a wavefunction that is neither of its components but rather a superposition of them, just as in the vector analogy above (which is formally equivalent to this situation).
In benzene both Kekulé structures have equal weight, but this need not be the case. In general, the superposition is written with undetermined constant coefficients, which are then variationally optimized to find the lowest possible energy for the given set of basis wavefunctions. This is taken to be the best approximation that can be made to the real structure, though a better one may be made with addition of more structures.
In molecular orbital theory, the main alternative to VB, resonance often (but not always) translates to a delocalization of electrons in pi orbitals (which are a separate concept from pi bonds in VB). For example, in benzene, the MO model gives us 6 pi electrons completely delocalised over all 6 carbon atoms, thus contributing something like half-bonds. This MO interpretation has inspired the picture of the benzene ring as a hexagon with a circle inside. Often when describing benzene the VB picture and the MO picture are intermixed, talking both about sigma 'bonds' (strictly a concept from VB) and 'delocalized' pi electrons (strictly a concept from MO).
Resonance energy
Resonance hybrids are always more stable than any of the canonical structures would be, if they existed[1]. The delocalization of the electrons lowers the orbital energies, imparting this stability. The resonance in benzene gives rise to the property of aromaticity. The gain in stability of the resonance hybrid over the most stable of the (non-existent) canonical structures is called the resonance energy. A canonical structure that is lower in energy makes a relatively greater contribution to the resonance hybrid, or the actual picture of the molecule. In fact, resonance energy, and consequently stability, increase with the number of canonical structures possible, especially when these (non-existent) structures are equal in energy. Resonance energy of a conjugated system can be 'measured' by heat of hydrogenation of the molecule. Consider the example of benzene. The energy required to hydrogenate an isolated pi-bond is around 28.6 kcal/mol (120 kJ/mol). Thus, according to the VB picture of benzene (having three pi-bonds), the complete hydrogenation of benzene should require 85.8 kcal/mol (360 kJ/mol). However, the experimental heat of hydrogenation of benzene is around 49.8 kcal/mol (210 kJ/mol). The difference of 36 kcal/mol (150 kJ/mol) can be looked upon as a measure of resonance energy. One must bear in mind again that resonance structures have no physical existence. So, even though the term 'resonance energy' is quite meaningless, it offers an insight into how different the VB picture of a molecule is from the actual molecule itself. The resonance energy can be used to calculate electronegativities on the Pauling scale.
Writing resonance structures
- Position of nuclei must be the same in all structures, otherwise they would be isomers with real existence.
- Total number of electrons and thus total charge must be constant.
- When separating charge (giving rise to ions), usually structures where negative charges are on less electronegative elements have little contribution, but this may not be true if additional bonds are gained.
- Resonance hybrids can not be made to have lower energy than the actual molecules.
History
The concept of resonance was introduced by Linus Pauling in 1928. The term "resonance" came from the analogy between the quantum mechanical treatment of the H2 molecule and a classical system consisting of two coupled oscillators. In the classical system, the coupling produces two modes, one of which is lower in frequency than either of the uncoupled vibrations; quantum-mechanically, this lower frequency is interpreted as a lower energy. The alternative term mesomerism popular in German and French publications with the same meaning was introduced by Christopher Ingold in 1938 but did not catch on in the English literature. The current concept of mesomeric effect has taken on a related but different meaning. The double headed arrow was introduced by the German chemist Arndt (also responsible for the Arndt-Eistert synthesis) who preferred the German phrase zwischenstufe or intermediate phase.
Due to confusion with the physical meaning of the word resonance, as no elements actually appear to be resonating, it has been suggested that the term resonance be abandoned in favor of delocalization.[2] Resonance energy would become delocalization energy and a resonance structure becomes a contributing structure. The double headed arrows would be replaced by commas.
Examples
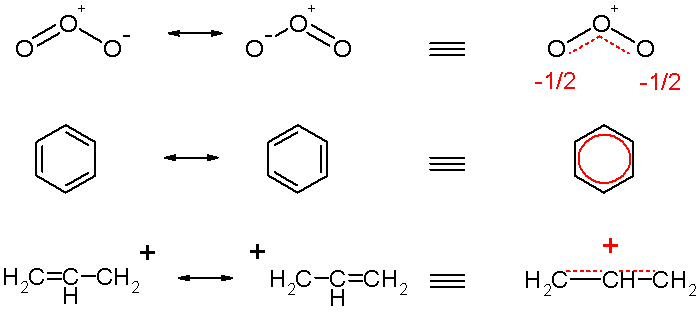
The ozone molecule is represented by two resonance structures in the top of scheme 2. In reality the two terminal oxygen atoms are equivalent and the hybrid structure is drawn on the right with a charge of -1/2 on both oxygen atoms and partial double bonds.
The concept of benzene as a hybrid of two conventional structures (middle scheme 2) was a major breakthrough in chemistry made by Kekulé, and the two forms of the ring which together represent the total resonance of the system are called Kekulé structures. In the hybrid structure on the right the circle replaces three double bonds.
Reactive intermediates
Often, reactive intermediates such as carbocations and free radicals have more delocalised structure than their parent reactants, giving rise to unexpected products. The classical example is allylic rearrangement. When 1 mole of HCl adds to 1 mole of 1,3-butadiene, in addition to the ordinarily expected product 3-chloro-1-butene, we also find 1-chloro-2-butene. Isotope labelling experiments have shown that what happens here is that the additional double bond shifts from 1,2 position to 2,3 position in some of the product. This and other evidence (such as NMR in superacid solutions) shows that the intermediate carbocation must have a highly delocalised structure, different from its mostly classical (delocalisation exists but is small) parent molecule. This cation (an allylic cation) can be represented using resonance, as shown above.
This observation of greater delocalisation in less stable molecules is quite general. The excited states of conjugated dienes are stabilised more by conjugation than their ground states, causing them to become organic dyes.
An well-studied example of delocalisation that does not involve pi electrons (hyperconjugation) can be observed in the non-classical ion norbornyl cation. Other examples are diborane and methonium (CH5+). These are known as 3-center-2-electron bonds and are represented either by resonance structures involving rearrangement of sigma electrons or by a special notation, a Y that has the three nuclei at its three points.
See also
References
- ↑ Robert Morrison, Robert Boyd (1989). "Chapter 10". Organic Chemistry (Fifth Edition ed.). Prentice Hall of India. pp. Page 372. ISBN 0-87692-560-3.
The resonance hybrid is more stable than any of the contributing structures.
- ↑ If It's Resonance, What Is Resonating? Kerber, Robert C. . J. Chem. Educ. 2006 83 223. Abstract
Template:WikiDoc Sources
Template:Jb1
de:Mesomerie it:Risonanza (chimica) he:רזוננס כימי nl:Resonantie (scheikunde) sv:Resonans (kemi)